Lambda calculus and Lambda expressions in functional programming

Lambda calculus 

lambda calculus is a framework,foundation of functional programming.

Developed by Alonzo church,1941

lambda expression defines, 

• function parameters
• body

Dose NOT define a name; lambda is the nameless function.

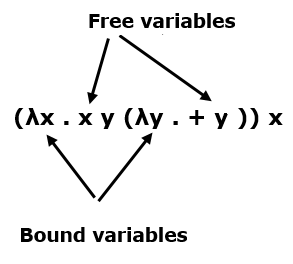
Below x define a parameter for the unnamed function

The notation λx.E to denote a function in which ‘x’ is a formal argument and ‘E’ is the functional body. These functions can be of without names and single arguments.

The notation E₁.E₂to denote the application of function E₁ to actual argument E₂. And all the functions are on single argument.


Lamdba calculus includes three different types of expressions, 

E :: = x(variables)

| E1 E2(function application)

| λx.E(function creation)

Where λx.E is called Lambda abstraction and E is known as λ-expressions.

Alpha reduction is very simple and it can be done without changing the meaning of a lambda expression.

The Church-Rosser Theorem states the following −

• If E1 ↔ E2, then there exists an E such that E1 → E and E2 → E. “Reduction in any way can eventually produce the same result.”
• If E1 → E2, and E2 is normal form, then there is a normal-order reduction of E1 to E2. “Normal-order reduction will always produce a normal form, if one exists.”